Narzędzia użytkownika
Spis treści
Wzorzec projektowy interpreter
Wzorzec projektowy interpretera korzysta z reprezentacji gramatyki analizowanego języka formalnego w celu interpretacji wyrażeń w tym języku. Wykorzystywany jest, gdy możliwe jest zapisanie zadań (problemów) w prostym, sformalizowanym języku. Rozwiązanie problemu polega wtedy na odpowiedniej interpretacji wyrażenia tego języka.
Typowe możliwości wykorzystania:
- interpretacja języków (programowania, matematycznych) w kompilatorach, interpreterach
- dopasowywanie wzorców, np. opisanych za pomocą wyrażeń regularnych
- inne, dające się formalnie opisać problemy, np. walidacja/interpretacja wyrażeń (pakietów) protokołów komunikacyjnych
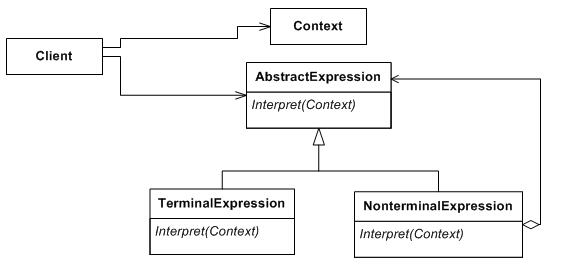
Struktura
AbstractExpression
Klasa abstrakcyjna wyrażeń. Z nich składa się wyrażenie w analizowanym języku.
TerminalExpression
Wyrażenie (symbol) terminalne w danej gramatyce, czyli wyrażenie, które nie składa się z podwyrażeń. Przykładowo, dla gramatyki wyrażeń arytmetycznych liczby są terminalami.
NonterminalExpression
Wyrażenie składające się (dające się podzielić) na podwyrażenia (terminalne lub nie). Na przykład dla gramatyki wyrażeń arytmetycznych takim wyrażeniem jest „3 + 5”.
Context
Aktualny kontekst, który przechowuje stan, w którym znajduje się w danym momencie interpreter, co dla gramatyk kontekstowych pozwala m.in. decydować jak na danym etapie należy interpretować dalsze elementy ciągu wejściowego. Kontekst jest globalnym elementem interpretera. Na przykład analizując kolejne cyfry liczby dziesiętnej kontekst może reprezentować miejsce dziesiętne, np. dziesiątki, setki itd.
Client
Tworzy drzewo wyrażenia, reprezentujące konkretne zdanie wejściowe w języku zdefiniowanym przez gramatykę. Drzewo to jest budowane z konkretnych instancji wyrażeń terminalnych i nieterminalnych. Następnie wywołuje operację interpretacji na korzeniu tego drzewa.
Zagadnienia implementacyjne
Podstawowe kroki implementacji
- Tworzenie klas wyrażeń - każde wyrażenie terminalne i nieterminalne jest reprezentowane przez inną klasę pochodną od typu Expression (a właściwie od typów NonterminalExpression i TerminalExpression). Na przykład dla języka wyrażeń arytmetycznych mogą powstać m.in. klasy WyrażenieSuma, WyrażenieRóżnica - pochodne od NonterminalExpression, oraz WyrażenieLiczba - pochodne od klasy TerminalExpression. Należy wziąć pod uwagę, że tworzenie klas dla wszystkich możliwych wyrażeń terminalnych może być kłopotliwe ze względu na ich ilość, więc warto rozpatrzyć w tym przypadku stworzenie ogólniejszych klas, np. dla wyrażeń arytmetycznych zamiast oddzielnej klasy dla każdej możliwej liczby, można stworzyć jedną klasę Liczba, zawierającą jej wartość.
- Tworzenie klasy kontekstu - w przypadku wyrażeń arytmetycznych powinien on przechowywać bieżącą (do tej pory obliczoną) wartość wyrażenia i zależności pomiędzy danym wyrażeniem, a jego sąsiadami.
- Tworzenie drzewa zdania - nie jest zaliczane do zagadnienia wzorca interpretera, zazwyczaj realizowane przez zewnętrzny parser.
- Definiowanie funkcji interpretującej - zazwyczaj jako metody klasy podstawowej AbstractExpression. Nie zawsze jest konieczne, aby była ona wirtualna (wystarczy, aby korzystała ona z innych metod wirtualnych w danej klasie - patrz przykład poniżej). Jeśli jednak zajdzie taka potrzeba, warto rozpatrzyć możliwość zastosowania wzorca Wizytatora.
Opcjonalne zagadnienia
- Akcje domyślne - przydatne może być określenie domyślnego wyniku interpretacji w klasie podstawowej wyrażenia dla wyrażeń nie mających konkretnego efektu (np. tylko służących do rozwijania podwyrażeń i oddających dalszą kontrolę tym podwyrażeniom).
- Wyrażenia współdzielone - możliwe jest wielokrotne użycie instancji danego wyrażenia (np. konkretnej liczby) dla wielu wyrażeń w celu oszczędności pamięci. Na przykład dla wyrażenia „2 + 5 - 2” można dwukrotnie skorzystać z klasy reprezentującej terminal „2”. Należy przy tym pamiętać, aby nie zapamiętywać stanu (kontekstu) w klasie wyrażenia, gdyż zazwyczaj jest on różny na różnych etapach interpretacji.
- Wielowątkowość - jeśli możliwe jest rozwiązywanie podwyrażeń w oddzielnych wątkach.
Przydatność
Wzorzec interpretera działa najlepiej, gdy:
- gramatyka jest stosunkowo prosta - dla skomplikowanych gramatyk hierarchia klas staje się duża i trudna w utrzymaniu.
- efektywność nie jest cechą krytyczną
- istotna jest możliwość łatwej zmiany i rozszerzania gramatyki - wystarczy dodać nowe klasy do hierarchii lub zmodyfikować istniejące
Przykład
Prosty program wykorzystujący wzorzec interpretera do konwersji stringów zawierających liczby rzymskie na liczby typu integer. Ponieważ system rzymski korzysta z różnych symboli dla poszczególnych potęg liczby 10, wyrażeniami są tutaj klasy reprezentujące różne zachowania dla Tysięcy, Setek, Dziesiątek i Jedności. Kontekst jest zrealizowany w sposób uproszczony: poprzez przekazywanie wejściowego ciągu znaków jako argumentu funkcji interpretuj() oraz zwracanie sumy danego wyrażenia. W bardziej złożonej implementacji kontekst mógłby być zrealizowany przez stworzenie oddzielnej klasy, zawierającej dwa pola: ciąg, przechowującej aktualny ciąg wejściowy i suma, przechowującej wartość wyrażenia na danym etapie interpretacji. Klasa ta musiałaby być przekazywana do kolejnych klas wyrażeń, jako argument funkcji interpretuj().
Również drzewo wyrażenia jest uproszczone i w tym przypadku jest ono po prostu listą.
#include <iostream> #include <string> #include <boost/algorithm/string/predicate.hpp> #include <boost/foreach.hpp> #include <boost/ptr_container/ptr_list.hpp> /** Reprezentuje (pod)wyrazenie, bedace czescia ciagu cyfr liczby rzymskiej. * Kazde wyrazenie rozni sie aktualnym kontekstem, ktory jest * analogia "miejsca dziesietnego" w danej liczbie rzymskiej. * Od miejsca zaleza symbole dla poszczegolnych "cyfr" oraz mnoznik, czyli * np. w kontekscie "setek" symbol "D" reprezentuje "piec" z mnoznikiem 100, * czyli 500. * W ogolnosci liczba rzymska sklada sie z cyfr, ktore * sumuja sie do wartosci calej liczby, a takze z cyfr, ktore * modyfikuja nastepujace po nich cyfry tworzac "podwojne" cyfry. * (np. "IX" jest "podwojna" cyfra, a "V" pojedyncza). */ class Wyrazenie : boost::noncopyable { public: /** Zwraca wartosc kolejnego, znajdujacego sie na poczatku ciagu s, * wyrazenia, w zaleznosci od aktualnego kontekstu. * Usuwa wykorzystane w aktualnym kroku cyfry z ciagu. */ int interpretuj( std::string & s ); /** Zwracaja symbole cyfr dla konkretnego - zaleznego od konkretnej * klasy pochodnej - kontekstu (miejsca w liczbie). * Mamy cztery rodzaje cyfr w systemie rzymskim: jeden, cztery, * piec i dziewiec. Odpowiedniki pozostalych cyfr arabskich sa * tworzone przez sumowanie w/w cyfr. * W systemie dziesietnym znaki odpowiadajace cyfrom sa zawsze takie * same, "1" jest taka sama dla jednosci, dziesiatek, setek itd. * Natomiast w systemie rzymskim "1" rozni sie w zaleznosci * od kontekstu: "I" dla jednosci, "X" dla dziesiatek itd. */ virtual std::string jeden() = 0; virtual std::string cztery() = 0; virtual std::string piec() = 0; virtual std::string dziewiec() = 0; /** Mnoznik, przez ktory nalezy pomnozyc wynikowa cyfre w danym * kontekscie. Analogia do mnozenia kolejnych cyfr liczby dziesietnej * przez kolejne potegi 10. */ virtual int mnoznik() = 0; }; /** Oblicza wartosc wszystkich cyfr w danym kontekscie (miejscu w liczbie), * czyli np. dla wszystkich cyfr skladajacych sie na setki * i usuwa wykorzystane cyfry z ciagu. */ int Wyrazenie::interpretuj( std::string & s ) { /** Sprawdza, czy ciag wejsciowy zaczyna sie od podanego podciagu. */ using boost::algorithm::istarts_with; if ( s.length() == 0 ) return 0; /** Suma cyfr dla danego kontekstu */ int suma = 0; /* Mamy dwa rodzaje cyfr podwojnych - dziewiec i cztery. * W jednym kontekscie zadne inne cyfry nie moga wystapic z * nimi rownoczesnie. */ if ( istarts_with( s, dziewiec() ) ) { /* Usun dwa pierwsze znaki cyfry podwojnej z ciagu */ s.erase( 0, 2 ); suma += 9 * mnoznik(); /* Po dziewiatce (i podobnie po czworce) nie moga wystapic * inne cyfry w jednym kontekscie, wiec mozemy wyjsc od razu */ return suma; } else if ( istarts_with( s, cztery() ) ) { s.erase( 0, 2 ); suma += 4 * mnoznik(); return suma; } else if ( istarts_with( s, piec() ) ) { s.erase( 0, 1 ); suma += 5 * mnoznik(); /* Po piatce natomiast moga wystapic jedynki, wiec * nie mozemy wyjsc przedwczesnie */ } /* Jedynki jako jedyne moga wystapic wielokrotnie po sobie * w jednym kontekscie, np. dla "III" zostanie * trzykrotnie usuniety symbol jedynki i trykrotnie do sumy dodane * zostanie 1 * mnoznik, czyli po prostu mnoznik. */ while ( istarts_with( s, jeden() ) ) { s.erase( 0, 1 ); suma += mnoznik(); } return suma; } /** Konkretne klasy dla danego kontekstu. * Zwracaja symbole cyfr o konkretnym znaczeniu w danym kontekscie, * na przyklad "czworka" dla jednosci jest "IV", a dla setek "CD". */ class Tysiace : public Wyrazenie { public: std::string jeden() { return "M"; } std::string cztery() { return " "; } std::string piec() { return " "; } std::string dziewiec() { return " "; } int mnoznik() { return 1000; } }; class Setki : public Wyrazenie { public: std::string jeden() { return "C"; } std::string cztery() { return "CD"; } std::string piec() { return "D"; } std::string dziewiec() { return "CM"; } int mnoznik() { return 100; } }; class Dziesiatki : public Wyrazenie { public: std::string jeden() { return "X"; } std::string cztery() { return "XL"; } std::string piec() { return "L"; } std::string dziewiec() { return "XC"; } int mnoznik() { return 10; } }; class Jednosci : public Wyrazenie { public: std::string jeden() { return "I"; } std::string cztery() { return "IV"; } std::string piec() { return "V"; } std::string dziewiec() { return "IX"; } int mnoznik() { return 1; } }; int main() { /* 2938 */ std::string rzymska( "MMCMXXXVIII" ); /* Stworzenie gramatyki liczb rzymskich, w ktorej wystepuja, * w kolejnosci, cyfry skladajace sie na: tysiace, setki, dziesiatki * i jednosci. W ten sposob kazda sekwencja znakow jest inaczej * interpretowana, w zaleznosci do tego, na jakim miejscu znajduje * sie w ciagu. * Tworzenie listy ma tylko na celu ulatwienie dalszego korzystania. * Ponadto jest to tylko jedna z mozliwosci, czesto korzysta sie z gramatyk * opartych o struktury drzewiaste. */ boost::ptr_list< Wyrazenie > wyrazenia; wyrazenia.push_back( new Tysiace() ); wyrazenia.push_back( new Setki() ); wyrazenia.push_back( new Dziesiatki() ); wyrazenia.push_back( new Jednosci() ); int suma = 0; /* Przeanalizuj cale wyrazenie dla kolejnych kontekstow zgodnie z gramatyka. * Kolejno dla kazdego kontekstu przeanalizuj poczatek ciagu i usun * wykorzystane cyfry, dodajac do sumy aktualnie obliczane wyrazenia. Ciag * jest przetwarzany zgodnie z wczesniej ustalonym porzadkiem przy tworzeniu * listy (gramatyki) wyrazen, poczawszy od tysiecy po jednosci. */ BOOST_FOREACH( boost::ptr_list< Wyrazenie >::reference w, wyrazenia ) { /* Wywoluje interpretuj() dla konkretnego potomka klasy Wyrazenie * (dziala mechanizm funkcji wirtualnych) */ suma += w.interpretuj( rzymska ); } assert( suma == 2938 ); std::cout << suma << std::endl; return 0; }